Число Фибоначчи
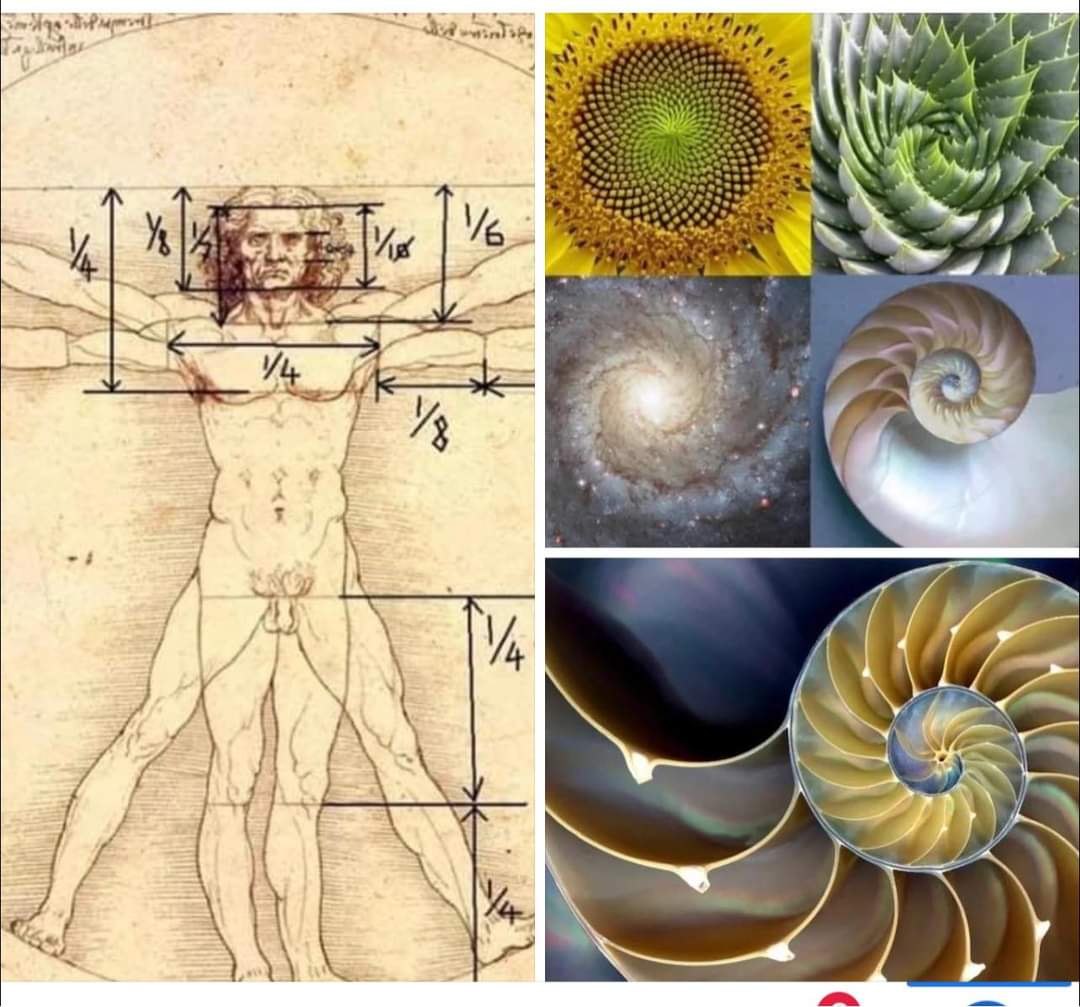
Почему оно так популярно в природе? Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении. Кто такой Фибоначчи? Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор. В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.
Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.
Числа Фибоначчи и золотое сечение Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение». Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах. Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником. Почему эта последовательность настолько уникальна Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.
Числа Фибоначчи в природе Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.
Последовательность Фибоначчи можно также увидеть в форме или разделении ветвей дерева. Основной ствол будет расти до тех пор, пока он не создаст ветвь, которая создает две точки роста. Затем один из новых стеблей разветвляется на два, в то время как другой находится в состоянии покоя. Такая картина ветвления повторяется для каждого из новых стеблей. Корневая система и даже водоросли также демонстрируют эту закономерность. Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов. Числа Фибоначчи в теле человека Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.
Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.
Источник Мировая История, Культура и Искусство
Поделитесь записью с друзьями
10 МИФОВ О РАБОТЕ НА СЕБЯ
Существует так много мифов о работе на себя (особенно между пожизненных служащих), что для начала хорошо было бы развеять некоторые из них.
Свой первый бизнес я начал сразу
Существует так много мифов о работе на себя (особенно между пожизненных служащих), что для начала хорошо было бы развеять некоторые из них.
Свой первый бизнес я начал сразу
Посмотреть ещё 8 фотографий
Обязанности кота
Посмотреть ещё 7 фотографий
Коты, уснувшие в самых неподходящих местах
#интересаради@
#интересаради@
© 2008‒2024 Социально‐развлекательная сеть «Фотострана». Пользователей: 25 670 750 человек
Следующая запись: Я — твоя Несудьба… Ты — моё «не дано»…
Лучшие публикации